LSTM은 RNN의 변형이고, GRU는 LSTM의 변형이라고 할 수 있습니다.
RNN Cell의 문제점
1. BPTT(BackPropagation Through Time)의 문제점
RNN에서의 역전파 방법인 BPTT는 아래의 그림과 같이 모든 타임스텝마다 처음부터 끝까지 역전파합니다.

그렇기 때문에 타임 스텝이 클 경우 RNN을 위와 같이 펼치게 되면 매우 깊은 네트워크가 됩니다. 이러한 네트워크는 vanishing & exploding gradient 문제가 발생할 가능성이 큽니다. 또한 계산량이 많기 때문에 한 번 학습하는데 아주 오랜 시간이 걸린다는 문제가 있습니다.
Truncated BPTT
-BPTT의 문제를 해결하기 위해 등장한 방법입니다.
-아래 그림과 같이 타임 스텝을 일정 구간(일반적으로 5-steps)으로 나누어 역전파를 계산하여 전체 역전파로 근사시키는 방법입니다.
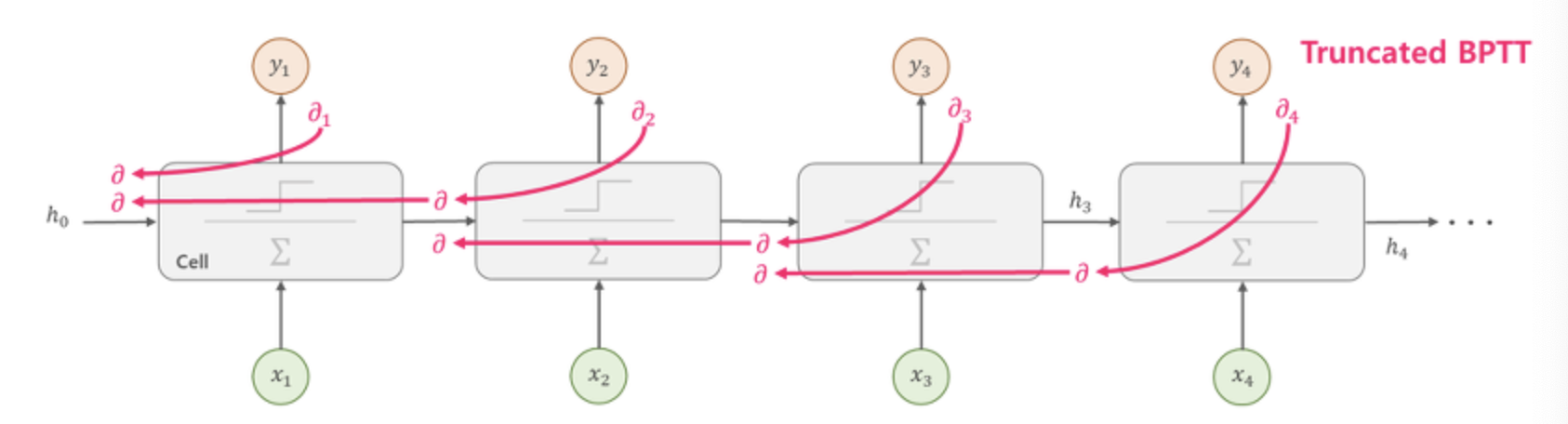
그러나 Truncated BPTT는 만약 학습 데이터가 장기간에 걸쳐 패턴이 발생한다고 하면, 이런 장기간(Long-Term)의 패턴을 학습할 수 없다는 문제가 있습니다.
2. 장기 의존성(Long-Term Dependency) 문제
-RNN은 타입 스텝 t에서 이전 타임 스텝 t-1의 상태(state, $h_{t-1}$)를 입력으로 받는 구조이기 때문에 이전의 정보가 현재의 타임 스텝 t에 영향을 줄 수 있습니다. 따라서 RNN의 순환 뉴런(Reccurent Neurons)의 출력은 이전 타임 스텝의 모든 입력에 대한 함수입니다. 이를 메모리 셀(Memory Cell)이라고 합니다.
-장기 의존성 문제는 RNN은 이론적으로 모든 이전 타임 스텝이 다음 스텝에 영향을 주지만, 앞쪽의 타임 스텝(t=0, t=1 등)은 타임 스텝이 길어질수록 영향을 주지 못하는 문제가 발생하는 것을 의미합니다.
-입력 데이터가 RNN Cell을 거치면서 특정 연산을 통해 데이터가 변환되어, 일부 정보는 타임 스텝마다 사라지기 때문에 장기 의존성 문제가 발생하게 됩니다.
-이러한 문제를 해결하기 위해 장기간의 메모리를 가질 수 있는 여러 종류의 셀이 만들어졌는데, 그 중 대표적인 것들이 LSTM과 GRU 셀입니다.

LSTM Cell
LSTM(Long Short-Term Memory) 셀은 S.Hochreiter와 J.Schmidhuber가 1997년에 제안한 셀로, RNN 셀의 장기 의존성 문제를 해결할뿐만 아니라 학습 또한 빠르게 수렴합니다.
LSTM 셀의 구조
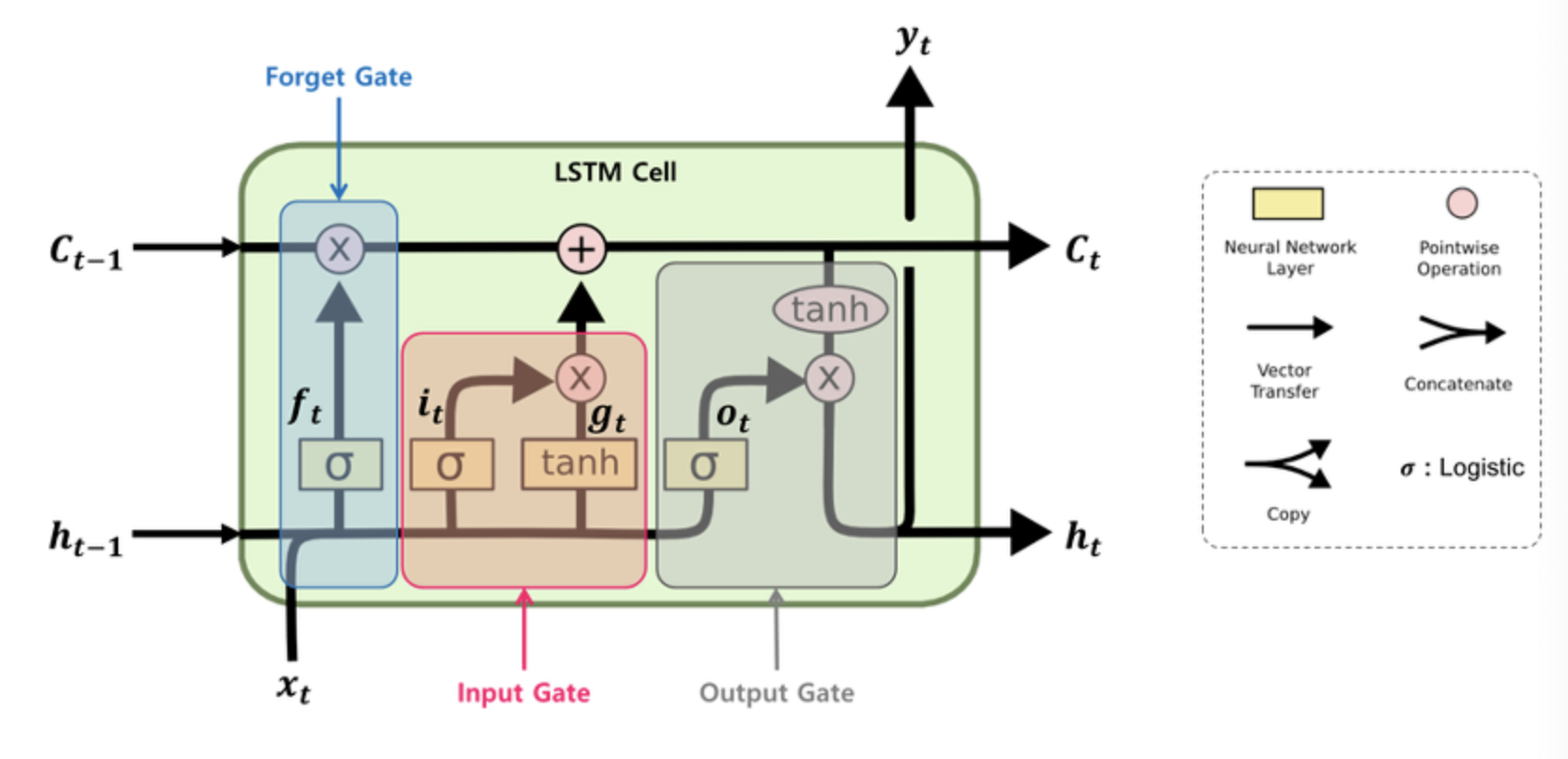
위의 그림에서 보면 LSTM 셀에서는 상태(state)가 두 개의 벡터 $h_t$와 $c_t$로 나누어진다는 것을 알 수 있습니다.
$h_t$: 단기 상태(short-term state)
$c_t$: 장기 상태(long-term state)
LSTM의 핵심은 네트워크가 장기 상태($c_t$)에서 기억할 부분, 삭제할 부분, 그리고 읽어들일 부분을 학습하는 것입니다.
LSTM Cell의 작동 방식
1. 장기기억 $c_{t-1}$은 셀의 왼쪽에서 오른쪽으로 통과하게 됩니다.
2. forget gate를 지나면서 일부 기억(정보)을 잃습니다.
3. 그 다음 덧셈(+) 연산으로 input gate로부터 새로운 기억의 일부를 추가합니다.
4. 이렇게 만들어진 $c_t$는 별도의 추가 연산 없이 바로 출력되며, 이러한 장기 기억 $c_t$는 타임 스텝마다 일부의 기억을 삭제하고 추가하는 과정을 거치게 됩니다.
5. 덧셈 연산 후에 $c_t$는 복사되어 output gate의 tanh함수로 전달되어 단기 상태 $h_t$와 셀의 출력인 $y_t$를 만듭니다.
각 Gate들의 작동 방식
현재 입력 벡터 $x_t$와 이전의 단기 상태 $h_{t-1}$이 네 개의 다른 FC-레이어(Fully Connected layer)에 주입되는데, 이 레이어는 모두 다른 목적을 가집니다.
- 주요 레이어는 $g_t$를 출력하는 레이어이며, 현재 입력 데이터 $x_t$와 이전 타임스텝의 단기 상태 $h_{t-1}$을 분석하는 역할을 합니다. LSTM 셀에서는 이 레이어의 출력인 $g_t$가 $i_t$의 곱셈(x) 연산 후 장기 상태 $c_t$에 일부분이 더해지게 됩니다. 반면에 기본 RNN 셀에서는 이 레이어만 있으며, 바로 $y_t$와 $h_t$로 출력됩니다.
- $f_t$, $i_t$, $o_t$를 출력하는 세 개의 레이어에서는 활성화 함수로 시그모이드(sigmoid, logistic)를 사용합니다. 시그모이드 함수의 출력 범위는 0~1이며, 이 출력값은 각 forget, input, output 게이트의 원소별(element-wise) 곱셈연산에 입력됩니다. 따라서 출력이 0일 경우에느 게이트를 닫고, 1일 경우에는 게이트를 열기 때문에 $f_t$, $i_t$, $o_t$를 gate controller라고 합니다.
1. Forget gate: $f_t$에 의해 제어되며 장기 상태 $c_t$의 어느 부분을 삭제할지를 제어합니다.
2. Input gate: $i_t$에 의해 제어되며 $g_t$의 어느 부분이 장기 상태 $c_t$에 더해져야 하는지를 제어합니다.
3. Output gate: $o_t$는 장기 상태 $c_t$의 어느 부분을 읽어서 $h_t$와 $y_t$로 출력해야 하는지를 제어합니다.
다음 식은 위의 그림의 타임스텝 t에서 셀의 장기 상태, 단기 상태, 그리고 각 레이어의 출력을 구하는 식을 나타낸 것입니다.
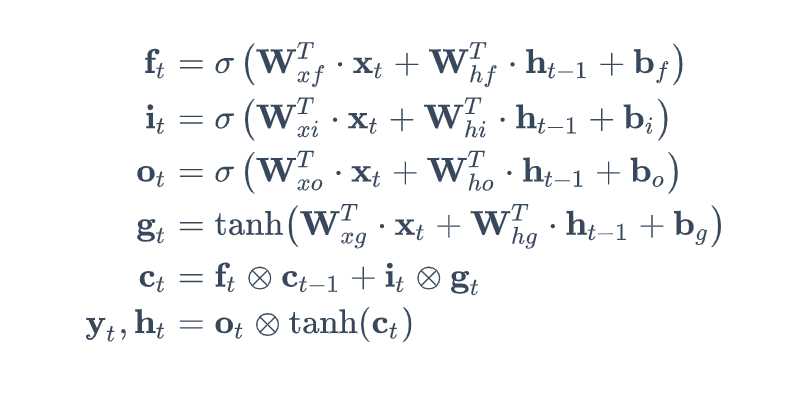
-$W_{xf}, W_{xi}, W_{x0}, W_{xg}$: 입력 벡터 $x_t$에 연결된 네 개의 레이어에 대한 가중치 행렬
-$W_{hf}, W_{hi}, W_{h0}, W_{hg}$: 이전 타임스텝의 단기 상태 $h_{t-1}$에 연결된 네 개의 레이어에 대한 가중치 행렬
-$b_f, b_i, b_0, b_g$: 네 개의 레이어에 대한 편향(bias)으로, 텐서플로우에서는 $b_f$를 1로 초기화하여 학습 시작시에 모든 것을 잃어버리는 것을 방지합니다.
GRU Cell
GRU(Gated Recurrent Unit) 셀은 2014년에 K. Cho(조경현) 등에 의해 제안된 LSTM 셀의 간소화된 버전이라고 할 수 있습니다.
GRU 셀의 구조

- LSTM Cell에서의 두 벡터 $c_t$와 $h_t$가 하나의 벡터 $h_t$로 합쳐졌습니다.
- 하나의 gate controller인 $z_t$가 forget과 input 게이트(gate)를 모두 제어합니다. $z_t$가 1을 출력하면 forget 게이트가 열리고 input 게이트가 닫히며, $z_t$가 0일 경우 반대로 forget 게이트가 닫히고 input 게이트가 열립니다. 즉, 이전(t-1)의 기억이 저장될 때마다 타임 스텝 t의 입력은 삭제됩니다.
- GRU 셀은 output 게이트가 없어 전체 상태 벡터 $h_t$가 타임 스텝마다 출력되며, 이전 상태 $h_{t-1}$의 어느 부분이 출력될지 제어하는 새로운 gate controller인 $r_t$가 있습니다.
GRU 셀의 상태(state)와 각 레이어의 출력을 계산하는 식은 다음과 같습니다.

'인공지능' 카테고리의 다른 글
| [Keras] to_categorial 함수 (0) | 2021.02.19 |
|---|---|
| [모두를 위한 딥러닝1] NN의 꽃 RNN 이야기(8주차) (0) | 2021.02.17 |
| [모두를 위한 딥러닝1] 여러가지 CNN 알고리즘(7주차_2) (0) | 2021.02.14 |
| [모두를 위한 딥러닝1] Convolutional Neural Networks(CNN)(7주차_1) (0) | 2021.02.14 |
| [모두를 위한 딥러닝1] Weight의 초기값 설정하기(6주차_2) (0) | 2021.02.04 |