multi-variable linear regression
x_data=[[73., 80., 75.], [93., 88., 93.],
[89., 91., 90.], [96., 98., 100.], [73., 66., 70.]]
y_data=[[152.], [185.], [180.], [196.], [142.]]
X=data[:, :-1]
Y=data[:, :[-1]]
W=tf.Variable(tf.random.normal([3,1]), name='weight')
b=tf.Variable(tf.random.normal([1]), name='bias')
learning_rate=0.001
hypothesis=tf.matual(X, W)+b
def predict(X):
return tf.matual(X, W)+b
for step in range(2001):
with tf.GradientTape() as tape:
cost=tf.reduce_mean(tf.square(predict(X)-Y))
W_grad, b_grad=tape.gradient(cost, [W, b])
w.assign_sub(learning_rate * W_grad)
b.assign_sub(learning_rate * b_grad)
if step%10==0:
print("(:5) | {:10.4f}".format(step, cost.numpy()))
Matrix
w1x1 + w2x2 + w3x3 + w4x4 + ... + wnxn
항이 무수히 많아질 때 이를 효율적으로 이용하기 위해 사용합니다.
Hypothesis using matrix
w1x1+w2x2+w3x3
$$\begin{pmatrix} x _{1} & x_{2} & x_{3} \end{pmatrix}\begin{pmatrix} w1 \\ w2 \\ w3 \end{pmatrix} = \begin{pmatrix} x_1w_1 + x_2w_2 + x_3w_3 \end{pmatrix}$$
$$H(x)=XW$$
위의 식에 해당되는 값이 하나의 인스턴스가 됩니다. (1x1)
하나 이상의 인스턴스들이 존재할 수 있는데, n개의 인스턴스가 존재할 경우, nx1 행렬이 됩니다.
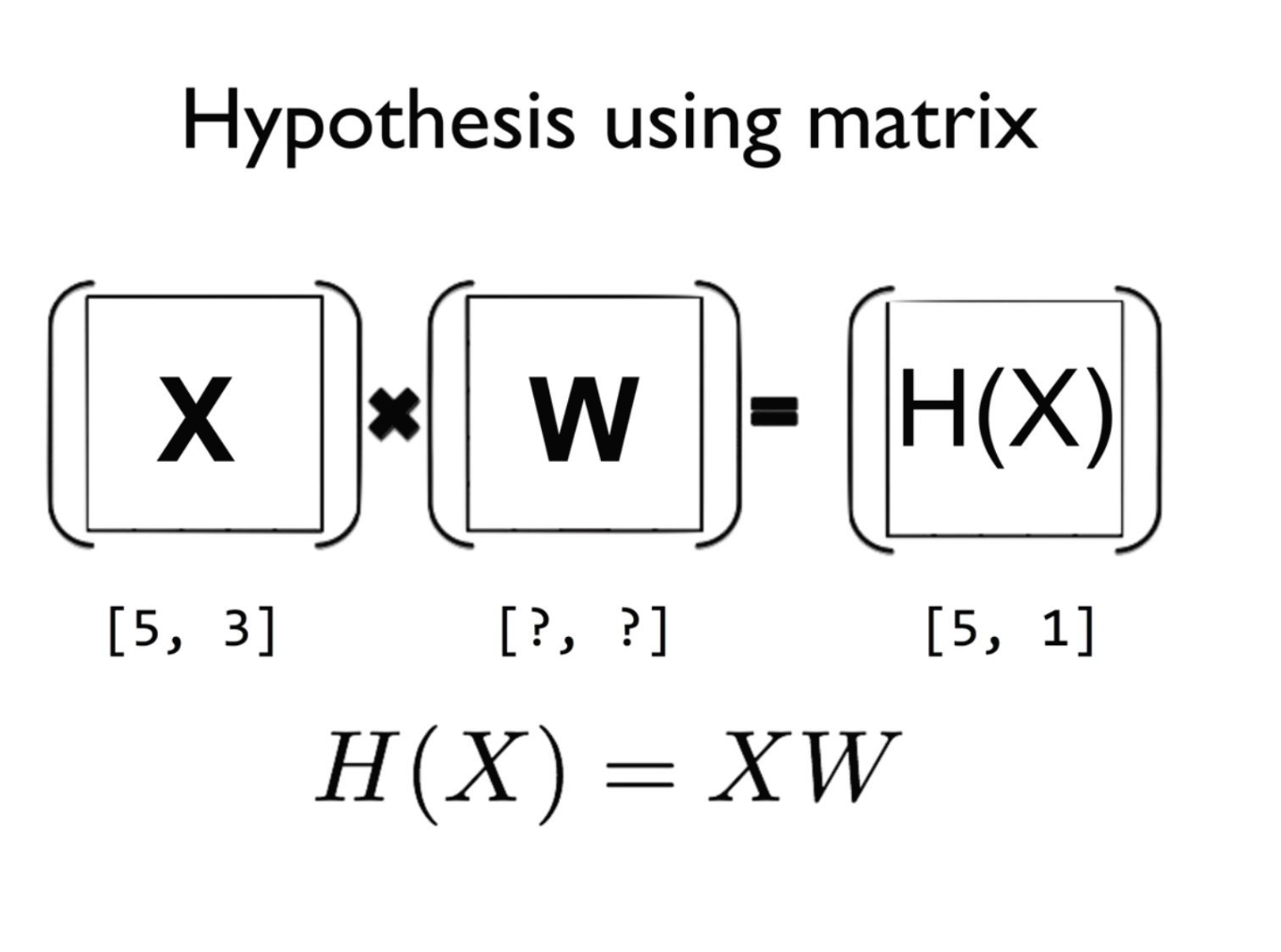
5: instance의 개수
3: x variable의 개수
1: y 값-> 1개 존재함
$$[n, m] * [m, 1] = [n, 1]$$
WX vs XW
-Lecture(theory): $H(x)=Wx+b$
-Implementation(Tensorflow): $H(x)=XW$
Logistic Classification의 가설 함수 정의
Classification
-Regression은 숫자를 예측하는 것이었다면, Classification은 정해진 것들 중에 고르는 것입니다.
-Binary Classification은 Classification 중에서도 정해진 '둘' 중에 하나를 고르는 것입니다.
ex) Spam Email Detection: Spam(1)/Ham(0)
ex) Facebook feed: show(1)/hide(0)
ex) 신용카드를 분실했을 때, 기존의 패턴을 벗어나는 소비가 이루어지는 경우 탐지: legitimate(0)/fraud(1)
ex) 주식 시장: buying(1)/selling(0)
ex) 시험: Pass(1)/Fail(0)
Binary Classification 구현 방법
-Linear Regression: 기준을 정하여 일정 기준 이상이면 1, 일정 기준 이하이면 0으로 정합니다.
-문제: 기준값을 머신러닝 학습시키면 어느 정도 오차가 발생합니다. 그렇게 되면 소수점 단위의 작은 오차로 인해 실제 Pass인 값이 Fail 값으로 바뀌어버릴 수 있습니다.
Logistic Hypothesis
$$H(x)=\frac{1}{1+e^{-W^TX}}$$
$W^TX$ : Linear Hypothesis 값을 대입한 것(WX)
Logistic Regression의 cost 함수 설명

$0<H(x)<1$
Logistic Regression의 cost 함수는 값이 0에서 1 사이가 되었습니다. 또한 그래프의 개형도 기존의 매끄러운 포물선 모양이 아니라, 구불구불한 형태로 바뀌었습니다.
Linear Regression 그래서에서는 포물선의 기울기가 0이 되는 부분이 최솟값이라는 것을 알 수 있었으나, Logistic Regression 그래프는 구불구불한 형태이므로 기울기가 0이 되는 부분이 1개 이상 나타날 수 있습니다. 따라서 시작 지점에 따라 최소점이 달라질 수 있습니다.
Local minimum: 시작점에 따라 달라지는 부분 최솟값
Global minimum: 전체 함수의 최솟값
학습이 Local minimum에서 멈춰버릴 경우 실제 함수의 최솟값을 알 수 없게 됩니다. 따라서 hypothesis을 바꿔줌과 함께 cost 함수도 바꿔주어야 합니다.
New cost function for logistic

$$H(x)=\frac{1}{1+e^{-W^TX}}$$
첫번째 C 함수에서
i) y=1일 때
예측이 맞았다면(y = H(x)), H(x)=1 -> cost(1)=0
예측이 틀렸다면(y $\ne$ H(x)), H(x)=0 -> cost(0)= $\infty$
ii) y=0일 때
예측이 맞았다면(y = H(x)), H(x)=0 -> cost(1)=0
예측이 틀렸다면(y $\ne$ H(x)), H(x)=1 -> cost(0)= $\infty$
예측이 틀릴 경우, cost 값이 매우 커져서 시스템에 부하가 발생할 수 있게 됩니다.
두번째 C 함수에서
i) y=1일 때, c=-log(H(x))
ii) y=0일 때, c=-log(1-H(x))
Minimize Cost - Gradient decent algorithm

'인공지능' 카테고리의 다른 글
| [Training Neural Network] epoch, batch, and iteration (0) | 2021.01.20 |
|---|---|
| [Optimizer] Optimizer의 종류 (0) | 2021.01.19 |
| [Keras] Keras에서 loss 함수 (0) | 2021.01.19 |
| [모두를 위한 딥러닝1] Soft classification(3주차) (0) | 2021.01.16 |
| [모두를 위한 딥러닝1] Linear Regression(1주차) (0) | 2021.01.07 |