소수(Prime Number)란 '양의 약수를 두 개만 가지는 자연수'를 말합니다. 이런 소수(Prime Number)를 구하기 위한 방법으로 가장 대표적인 것이 '에라토스테네스의 체' 입니다. '에라토스테네스의 체'를 이용하면 대량의 소수를 빠르고 정확하게 구할 수 있습니다.
1. 간단하게 소수를 판별하는 알고리즘 1
#include <iostream>
using namespace std;
int isPrimeNumber(int x) {
for(int i=2;i<x;i++) {
if(x%i==0) return false;
}
return true;
}위 알고리즘의 시간 복잡도는 O(n)입니다. 모든 경우를 다 돌며 약수인지 여부를 확인하기 때문에 매우 비효율적인 방법입니다. 그런데 두 수의 곱에서 서로 대칭을 이루는 경우를 빼면 시간 복잡도를 더 줄일 수 있습니다. 예를 들면 6의 경우 2*3=3*2와 같이 대칭을 이루고 있으므로, 특정한 숫자의 제곱근까지만 약수 여부를 검증하면 됩니다.
2. 간단하게 소수를 판별하는 알고리즘 2
#include <iostream>
#include <cmath>
using namespace std;
bool isPrimeNumber(int x) {
int end=(int)sqrt(x);
for(int i=2;i<=end;i++) {
if(x%i==0) return false;
}
return true;
}위 알고리즘의 시간 복잡도는 O(n^(1/2))입니다. 특정한 숫자의 제곱근까지만 약수 여부를 검증하기 때문에 1번보다 시간 복잡도를 더욱 줄일 수 있습니다. 그러나 대량의 소수를 한꺼번에 판별하고자 할 때에는 위의 방법들로 소수를 구하는 것이 여전히 비효율적입니다.
3. 에라토스테네스의 체
에라토스테네스의 체는 가장 먼저 소수를 판별할 범위만큼 배열을 할당하여 그 인덱스에 해당하는 값을 대입하여 초기화합니다.
1) 이차원 배열을 생성하여 값을 초기화합니다.
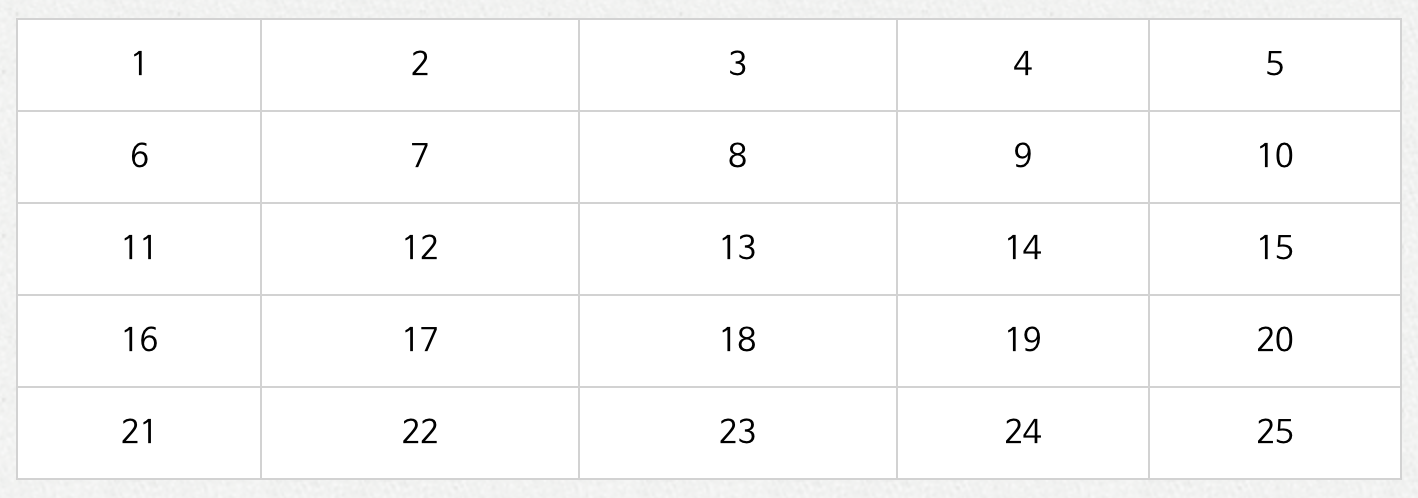
2) 2부터 시작하여 특정 숫자의 배수에 해당하는 숫자들을 모두 지웁니다. 이때, 자기 자신은 건너뜁니다.
<2의 배수>
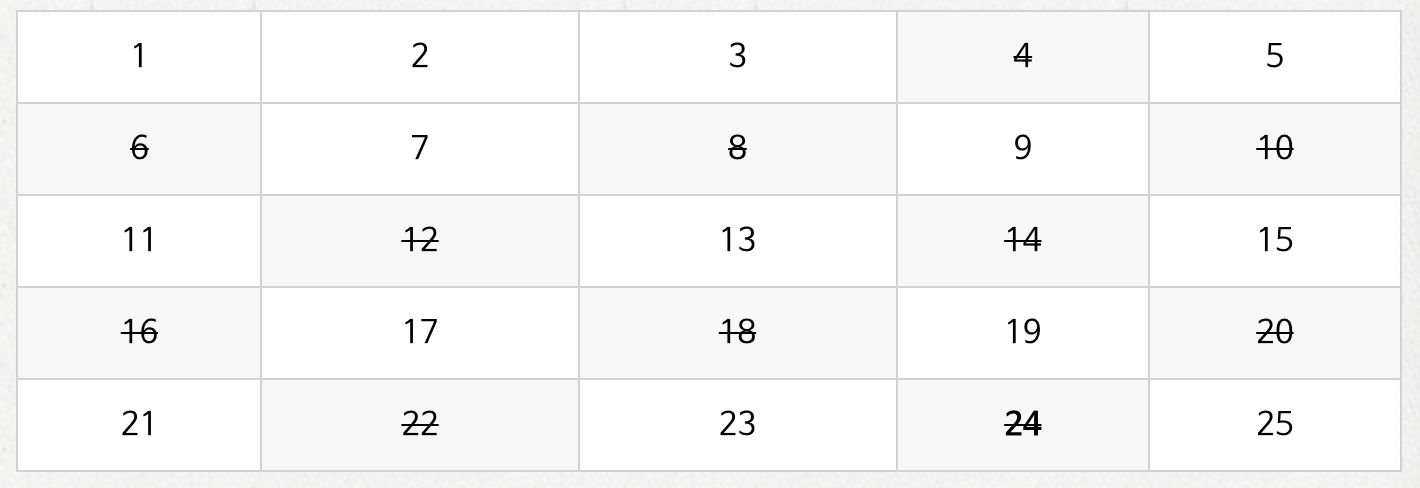
<3의 배수>
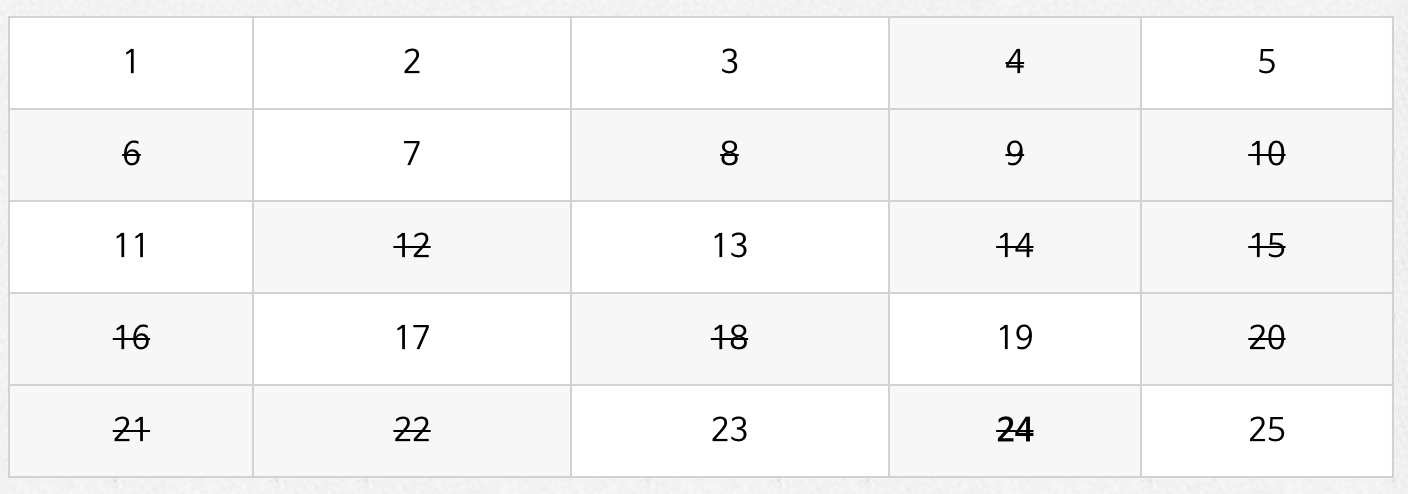
3) 이미 지워진 숫자는 건너뜁니다.
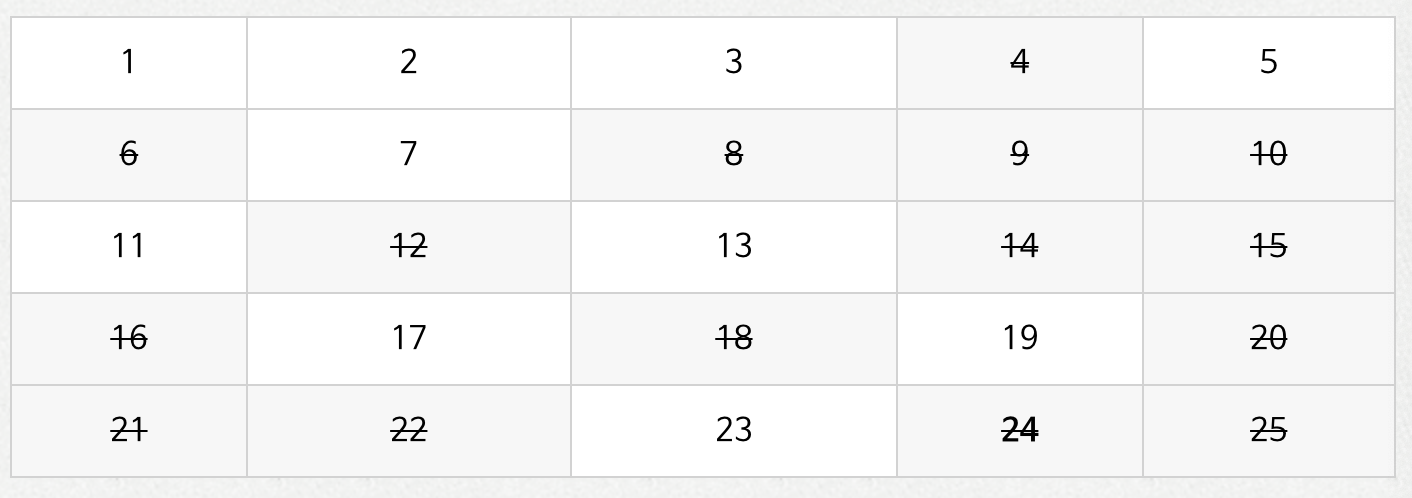
#include <iostream>
#include <cstring>
using namespace std;
bool a[4000001]={true,};
void primeNumber(int x) {
memset(a, true, sizeof(a));
for(int i=2;i<=x;i++) {
if(a[i]==true) {
for(int j=i+i;j<=x;j+=i) {
a[j]=false;
}
}
}
}
출처: https://blog.naver.com/PostView.naver?blogId=ndb796&logNo=221233595886&redirect=Dlog&widgetTypeCall=true&directAccess=false
'코딩테스트 > 기타' 카테고리의 다른 글
| [Python] 입출력 (0) | 2021.09.14 |
|---|---|
| [C/C++] 피보나치 수열 알고리즘(피사노 주기) (0) | 2021.08.25 |
| [C++] lower_bound(), upper_bound() 함수 (0) | 2021.06.28 |
| [C언어/C++] isspace 함수 (0) | 2021.06.24 |
| [C++] 알파벳 대소문자 변환 방법 2가지 (0) | 2021.06.24 |